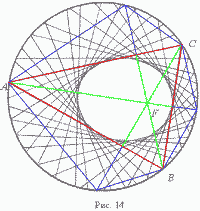
Постройте таких треугольников хотя бы десяток. Ничего не замечаете? Тогда постройте 100 таких треугольников! Теперь то вы заметили, что все эти треугольники касаются своими сторонами одного и того же эллипса! Причем одним фокусом этого эллипса является та самая наша точка М, а другим фокусом - центр окружности.
Сможете это доказать?
Заодно попробуйте доказать, что главная ось этого эллипса - прямая Эйлера для любого из построенных нами треугольников.




1 комментарий:
Спросите, как такой треугольник построить? Очень просто. Согните лист бумаги, на которой окружность так, чтобы линия окружности упала на эту точку М. Линия сгиба - искомая сторона треугольника.
Из точки М на эту сторону проведем перпендикуляр. Это высота нашего треугольника. Эта высота, пересекаясь с окружностью даст нам вершину треугольника.
Соединяем ее с двумя концами первой построенной стороны - вот и получили треугольник.
Докажите, что все высоты этого треугольника действительно пересекаются в точке М.
Теперь, зная эту процедуру, вы можете написать программу для компьютера для демонстрации этого замечательного факта.
Отправить комментарий