Обозначим точку пересечения медианы BD и отрезка AE.
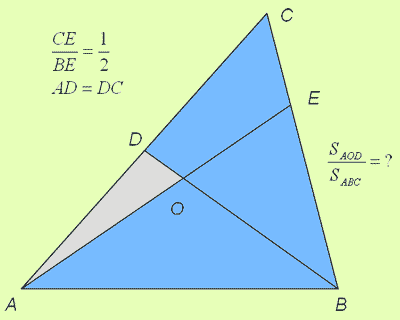
Надите отношение площади треугольника AOD к площади треугольника ABC.
Решите ту же задачу, если в треугольнике ABC отрезок BD - медиана, а точка Е делит сторону BC как n:m.
Подсказка: решение помещается на кусочке бумаги с той же площадью, что этикетка спичечного коробка.




1 комментарий:
Эх, помню решал подобные задачи, когда готовился поступать в инст :)
Помню, там надо было проводить дополнительное построение - отрезок, параллельный стороне треугольника, один конец которого лежит или в точке Е, или в D...
Отправить комментарий